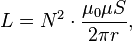Momotik.ru
Народный проект
Меню
Индуктивность
| Индуктивность | |
| Размерность |
L2MT−2I−2 |
|---|---|
| Единицы измерения | |
| СИ | |
| СГС | |
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле
— магнитный поток, — ток в контуре, — индуктивность.
- Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
- .
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
- .
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].
Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определенную эффективную индуктивность, используемую в расчетах полностью (хотя вообще говоря с определенными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
Содержание
|
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109 см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)[8]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Теоретическое обоснование
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[4].
Будем здесь вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля не настолько сильны и быстры, чтобы ими нельзя было пренебречь в смысле порождения ими магнитного поля.
Ток считаем одинаковым по всей длине контура (пренебрегая емкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).
По закону Био — Савара величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником также пропорционально порождающему току.
Рассуждение выше верно для вакуума. В случае присутствия магнитной среды[9] (магнетика) с заметной (или даже большой) магнитной восприимчивостью вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остается пропорциональным порождающему его току.
Тогда магнитный поток, то есть поток поля вектора магнитной индукции:
через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.
Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближенно рассчитать поток через нее (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).
Итак, мы обосновали:
- ~
этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что
В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть ее краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.
Но это действительно так: возьмем две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.
Свойства индуктивности
- Индуктивность[10] всегда положительна.
- Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника).[11]
Индуктивность одновиткового контура и индуктивность катушки
Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом[4]:
где — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду:
где — сумма магнитных потоков через все витки (это так называемый полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока вообще в случае для катушки в общем определении индуктивности и в теоретическом рассмотрении выше; однако для упрощения и удобства для многовитковых катушек в электротехнике пользуются отдельным понятием и отдельным обозначением), а — уже индуктивность многовитковой катушки. называют потокосцеплением или полным магнитным потоком[12]. Коэффициент пропорциональности иначе называется коэффициентом самоиндукции контура или просто индуктивностью[4].
Если поток, пронизывающий каждый из витков одинаков (что довольно часто можно считать верным для катушки в более или менее хорошем приближении), то . Соответственно, (суммарный магнитный поток через каждый виток увеличивается в N раз — поскольку его создают теперь N единичных витков, и потокосцепление еще в N раз, так как это поток через N единичных витков). Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.
Индуктивность соленоида
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока внутри катушки является фактически постоянной и (приближенно) равна
где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим[13], что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :
Отсюда следует формула для индуктивности соленоида (без сердечника):
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель — относительную магнитную проницаемость[14] сердечника:
В случае, когда , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника слишком во много раз.
Более точные формулы для соленоида конечного размера
Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[15]:


где
- - количество витков,
- - радиус цилиндра,
- - длина его образующей,
- ,
- ,
- - Эллиптические интегралы.
Это дает
- для
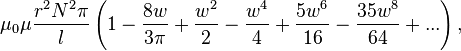
- для
Индуктивность тороидальной катушки (катушки с кольцевым сердечником)
Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближенно пользоваться формулой для бесконечного прямого соленоида (см. выше):
где - оценка длины соленоида ( - большой радиус тора).
Лучшее приближение дает формула
где предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.
Индуктивность длинного прямого проводника
Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближенной формулой[16]:
где − магнитная постоянная, - относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума ), - относительная магнитная проницаемость материала проводника, - длина провода, - радиус его сечения.
Индуктивность единичного круглого витка
Индуктивность витка в форме окружности[16] радиуса R из проводника круглого сечения радиусом r << R:
где − магнитная постоянная, - относительная магнитная проницаемость материала проводника.
Индуктивность прямоугольной рамки
Индуктивность прямоугольной рамки размерами из (достаточно тонкого) провода круглого сечения толщиной такова [17]:
где - диагональ прямоугольника.
См. также
Примечания
- ↑ Если контур многовитковый (катушка) или вообще сложной формы, поверхность, краем которой он будет являться, может иметь достаточно сложную форму. Это никак не сказывается на большей части общих утверждений, однако для упрощения конкретного понимания ситуации и количественных оценок в случае катушки обычно приближенно рассматривают эту поверхность как совокупность («стопку») отдельных листков, каждый из которых привязан к отдельному единичному витку, а общий поток через такую поверхность рассматривается приближенно как сумма потоков через все такие листки.
- ↑ Касаткин А. С. Основы электротехники. М:Высшая школа, 1986.
- ↑ Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. М:Высшая школа, 1978.
- ↑ Индуктивность // БСЭ
- ↑ Правда, этот случай в принципе выходит за рамки квазистационарного приближения, позволяющего рассматривать элементы схемы как независимые, то есть понятие индуктивности отдельного элемента цепи начинает терять четкий смысл; однако оно во всяком случае может быть использовано хотя бы для оценочного расчета.
- ↑ Прежде всего использование таких устройств, не основанных на электромагнитной индукции, обусловлено такими причинами, как необходимость или желательность иметь меньший размер элемента, чем это возможно для катушки индуктивности; например - в микросхемах, а также для элементов очень большой индуктивности.
- Генри (единица индуктивности) // БСЭ
- Генри Джозеф//БСЭ
- ↑ Присутствие магнетика особенно важно для катушек с ферромагнитным сердечником итп.
- ↑ Здесь имеется в виду настоящая индуктивность; в электронике можно создать искусственно элементы (не основанные на явлении самоиндукции), зависимость ЭДС в которых от производной тока будет такой же, как в катушке индуктивности, но с коэффициентом противоположного знака — такие элементы можно условно назвать (по их поведению в электрической цепи) элементами с отрицательной индуктивностью, однако они не имеют отношения к предмету данной статьи.
- ↑ Если считать структуру токов (точно или приближенно) фиксированной, то есть если токи не перераспределяются по объему проводника в процессе их возбуждения.
- Потокосцепление // БСЭ
- ↑ * Сивухин Д. В. Общий курс физики. — М.. — Т. III. Электричество.
- ↑ Как и в других случаях, присутствие магнетика, особенно если это ферромагнетик, для какового всегда имеет место гистерезис, приводит к более или менее существенной нелинейности (особенно большой для магнитожестких материалов сердечника); поэтому формулу для индуктивности, подразумевающей именно линейное приближение, следует считать вообще говоря лишь приближенной, в в качестве магнитной проницаемости в формулу входит некоторая эффективная величина, вообще говоря (а для ферромагнетиков как правило) зависящая от величины (или амплитуды) тока в катушке.
- ↑ Lorenz, L. (1879). «Über die Fortpflanzung der Elektrizität». Annalen der Physik VII: 161–193. (Индуктивность цилиндра с током, циркулирующим по его поверхности)..
- ↑ см.
- Moscow Power Engineering Institute: Mathcad Calculation Server
| Это заготовка статьи по физике. Вы можете помочь проекту, исправив и дополнив её. |
| Пассивные твердотельные | Резистор · Переменный резистор · Подстроечный резистор · Варистор · Конденсатор · Переменный конденсатор · Подстроечный конденсатор · Катушка индуктивности · Кварцевый резонатор · Предохранитель · Самовосстанавливающийся предохранитель · Трансформатор |
|---|---|
| Активные твердотельные | Диод · Светодиод · Фотодиод · Полупроводниковый лазер · Диод Шоттки · Стабилитрон · Стабистор · Варикап · Вариконд · Диодный мост · Лавинно-пролётный диод · Туннельный диод · Диод Ганна Транзистор · Биполярный транзистор · Полевой транзистор · КМОП-транзистор · Однопереходный транзистор · Фототранзистор · Составной транзистор · Баллистический транзистор Интегральная схема · Цифровая интегральная схема · Аналоговая интегральная схема Тиристор · Симистор · Динистор · Мемристор |
| Пассивные вакуумные | Бареттер |
| Активные вакуумные и газоразрядные | Электронная лампа · Электровакуумный диод · Триод · Тетрод · Пентод · Гексод · Гептод · Пентагрид · Октод · Нонод · Механотрон · Клистрон · Магнетрон · Амплитрон · Платинотрон · Электронно-лучевая трубка · Лампа бегущей волны |
| Устройства отображения | Электронно-лучевая трубка · ЖК-дисплей · Светодиод · Газоразрядный индикатор · Вакуумно-люминесцентный индикатор · Флажковый индикатор · Семисегментный индикатор |
| Акустические устройства и датчики | Микрофон · Громкоговоритель · Тензорезистор |
| Термоэлектрические устройства | Термистор · Термопара · Элемент Пельтье |