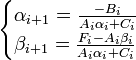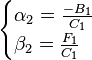Momotik.ru
Народный проект
Меню
Метки: Метод прогонки алгоритм, метод прогонки c++, метод прогонки как решать, метод прогонки уравнение пуассона.
Метод прогонки или алгоритм Томаса (англ. Thomas algorithm) используется для решения систем линейных уравнений вида , где A — трёхдиагональная матрица.
Содержание |
Описание метода
Система уравнений равносильна соотношению
Метод прогонки основывается на предположении, что искомые неизвестные связаны рекуррентным соотношением:
- где
Используя это соотношение, выразим xi-1 и xi через xi+1 и подставим в уравнение (1):
- ,
где Fi — правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать
Отсюда следует:
Из первого уравнения получим:
После нахождения прогоночных коэффициентов и , используя уравнение (2), получим решение системы. При этом,
Другим способом объяснения существа метода прогонки, более близким к терминологии конечно-разностных методов и объясняющим происхождение его названия, является следующий: преобразуем уравнение (1) к эквивалентному ему уравнению
c надиагональной (наддиагональной) матрицей
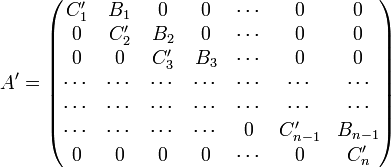 .
.
Вычисления проводятся в два этапа. На первом этапе вычисляются компоненты матрицы и вектора , начиная с до
и
На втором этапе, для вычисляется решение:
Такая схема вычисления объясняет также английский термин этого метода «shuttle».
Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.
Пример реализации на Си
Данный код работает при предположении, что a[0] = 0, b[n-1] = 0.
/**
* n - число уравнений (строк матрицы)
* b - диагональ, лежащая над главной (нумеруется: [0;n-2])
* c - главная диагональ матрицы A (нумеруется: [0;n-1])
* a - диагональ, лежащая под главной (нумеруется: [1;n-1])
* f - правая часть (столбец)
* x - решение, массив x будет содержать ответ
*/
void solveMatrix (int n, double *a, double *c, double *b, double *f, double *x)
{
double m;
for (int i = 1; i < n; i++)
{
m = a[i]/c[i-1];
c[i] = c[i] - m*b[i-1];
f[i] = f[i] - m*f[i-1];
}
x[n-1] = f[n-1]/c[n-1];
for (int i = n - 2; i >= 0; i--)
x[i]=(f[i]-b[i]*x[i+1])/c[i];
}
Литература
- Introduction to Numerical Methods in Chemical Engineering 1.1 "Tridiagonal matrix algorithm (TDMA)" (англ.)
Ссылки
- The Thomas Algorithm (англ.)
Tags: Метод прогонки алгоритм, метод прогонки c++, метод прогонки как решать, метод прогонки уравнение пуассона.