Momotik.ru
Народный проект
Меню
Метки: Математические символы скачать, математические символы буквы, математические символы дельта, математические символы округления, математические символы обозначения, математические символы в ворде, математические символы степени.
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования.
Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и
Знаки операций или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
К самым распространённым относятся:
- Плюс: +
- Минус: −
- Знаки умножения: ×, ∙ (в программировании также *)
- Знаки деления: :, ∕, ÷
- Знак равенства, приближённого равенства, неравенства: =, ≈, ≠
- Скобки (для определения порядка операций и др.): (), [], {}, <>
- Знак тождественности: ≡
- Знаки сравнения: <, >, ≤, ≥, ≪, ≫
- Знак порядка (тильда): ~
- Знак плюс-минус: ±
- Знак корня (радикал): √
- Факториал: !
- Знак интеграла: ∫
- Знак возведения в степень: ^ (в типографской и рукописной записи формул не применяется; используется в программировании, наряду с более редкими символами ↑ и **, а также в «линейной» текстовой записи формул).
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ |
Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). |
верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ |
Определение | означает « по определению равен ». означает « по определению равносильно » |
(Гиперболический косинус) (Исключающее или) |
|
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } |
Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} |
Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ |
Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » |
||
| «принадлежит», «из» «не принадлежит» |
||||
| Теория множеств | ||||
| ⊆ ⊂ |
Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). |
||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ |
Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). |
||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| "Пересечение … и … ", «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| "разность … и … «, „минус“, „… без …“ | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| „из … в“, | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| „отображается в“ | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| „Эн“ | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| „Зед“ | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| „Ку“ | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) |
|
| „Эр“ | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| „Це“ | ||||
| Числа | ||||
| H или | Кватернионы | означает множество | ||
| „Аш“ | ||||
| Числа | ||||
| „br /“ | Сравнение | обозначает, что строго меньше . означает, что строго больше . |
||
| „меньше чем“, „больше чем“ | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ |
Сравнение | означает, что меньше или равен . означает, что больше или равен . |
||
| „меньше или равно“; „больше или равно“ | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| „приблизительно равно“ | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| „Корень квадратный из …“ | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| „Плюс/минус бесконечность“ | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . |
||
| „Модуль“; „Мощность“ | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает „сумма , где принимает значения от 1 до “, то есть . означает сумму ряда, состоящего из . |
||
| „Сумма … по … от … до …“ | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает „произведение для всех от 1 до “, то есть | ||
| „Произведение … по … от … до …“ | ||||
| Арифметика | ||||
| ! | Факториал | означает „произведение всех натуральных чисел от 1 до включительно, то есть | ||
| “ факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
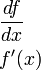 |
df/dx f'(x) |
Производная | или означает «(первая) производная функции от по переменной ». | |
| «Производная … по …» | ||||
| Математический анализ | ||||
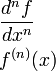 |
Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | ||
| «-я производная … по …» | ||||
| Математический анализ |
См. также
- Таблица обозначений абстрактной алгебры
- История математических обозначений
- Список математических аббревиатур
- Список обозначений в физике
Литература
- Выгодский М. Я. Справочник по элементарной математике. Изд. АСТ, 2003, ISBN 5-17-009554-6.
Ссылки
- Арифметические знаки // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
| Математические знаки | |
|---|---|
| Плюс ( + ) • Минус ( − ) • Знак умножения ( · или × ) • Знак деления ( : или / ) • Знак корня ( √ ) • Знак равенства ( =, ≈, ≡ и др.) • Знаки неравенства ( ≠, >, < и др.) • Бесконечность ( ∞ ) • Знак интеграла ( ∫ ) • Факториал ( ! ) • Вертикальная черта ( | ) • Знак градуса ( ° ) • Минута градуса ( ′ ) • Секунда градуса ( ″ ) • Штрих ( ′ ) • Звёздочка ( * ) • Обратная косая черта, бэкслеш ( \ ) • Процент ( % ) • Промилле ( ‰ ) • Тильда ( ~ ) • Циркумфлекс ( ^ ) • Плюс-минус ( ± ) • Обелюс ( ÷ ) • Десятичный разделитель ( , или . ) | |
| Математика • История математических обозначений |
| Это заготовка статьи по математике. Вы можете помочь проекту, исправив и дополнив её. |
Tags: Математические символы скачать, математические символы буквы, математические символы дельта, математические символы округления, математические символы обозначения, математические символы в ворде, математические символы степени.