Momotik.ru
Народный проект
Меню
Метки: Теория динамических систем учебник, теория динамических систем степаньянц, теория динамических систем мгу, теория динамических систем скачать.
Динамическая система — математическая абстракция, предназначенная для описания и изучения систем, эволюция во времени которых однозначно определяется начальным состоянием.
Содержание |
Введение
Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления.
Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое.
Различают системы с дискретным временем и системы с непрерывным временем.
В системах с дискретным временем, которые традиционно называются каскадами, поведение системы (или, что то же самое, траектория системы в фазовом пространстве) описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Каскады и потоки являются основным предметом рассмотрения в символической и топологической динамике.
Динамическая система (как с дискретным, так и с непрерывным временем) является по существу синонимом автономной системы дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям.
Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы).
Привлечение вероятностно-статистических представлений в эргодической теории динамических систем приводит к понятию динамической системы с инвариантной мерой.
Современная теория динамических систем является собирательным названием для исследований, где широко используются и эффективным образом сочетаются методы из различных разделов математики: топологии и алгебры, алгебраической геометрии и теории меры, теории дифференциальных форм, теории особенностей и катастроф.
Определение
Пусть — произвольное гладкое многообразие.
Динамической системой, заданной на гладком многообразии , называется отображение вида ( и ), которое является дифференцируемым отображением, причём — тождественное отображение пространства . В случае стационарных обратимых систем образует группу преобразований топологического пространства , а значит, в частности, для любых , выполняется тождество .
Из дифференцируемости отображения следует, что график функции (при ) является дифференцируемой функцией времени и называется интегральной траекторией (кривой) динамической системы. Её проекция на пространство , которое в таком случае носит название фазового пространства, называется фазовой траекторией (кривой) динамической системы.
Задание динамической системы, таким образом, эквивалентно разбиению фазового пространства на траектории.
Способы задания динамических систем
Для задания динамической системы необходимо описать её фазовое пространство , множество моментов времени и некоторое правило, описывающее движение точек фазового пространства со временем. Множество моментов времени может быть как интервалом вещественной прямой (тогда говорят, что время непрерывно), так и множеством целых или натуральных чисел (дискретное время). Во втором случае «движение» точки фазового пространства больше напоминает мгновенные «скачки» из одной точки в другую: траектория такой системы является не гладкой кривой, а просто множеством точек, и называется обычно орбитой. Тем не менее, несмотря на внешнее различие, между системами с непрерывным и дискретным временем имеется тесная связь: многие свойства являются общими для этих классов систем или легко переносятся с одного на другой.
Фазовые потоки
Пусть фазовое пространство представляет собой многомерное пространство или область в нем, а время непрерывно. Допустим, что нам известно, с какой скоростью движется каждая точка фазового пространства. Иными словами, известна вектор-функция скорости . Тогда траектория точки будет решением автономного дифференциального уравнения с начальным условием . Заданная таким образом динамическая система называется фазовым потоком для автономного дифференциального уравнения.
Каскады
Пусть — произвольное множество, и — некоторое отображение множества на себя. Рассмотрим итерации этого отображения, то есть результаты его многократного применения к точкам фазового пространства. Они задают динамическую систему с фазовым пространством и множеством моментов времени . Действительно, будем считать, что произвольная точка за время переходит в точку . Тогда за время эта точка перейдет в точку и т. д.
Если отображение обратимо, можно определить и обратные итерации: , и т. д. Тем самым получаем систему с множеством моментов времени .
Примеры
- Система дифференциальных уравнений
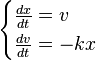
задает динамическую систему с непрерывным временем, называемую «гармоническим осциллятором». Её фазовым пространством является плоскость , где — скорость точки . Гармонический осциллятор моделирует разнообразные колебательные процессы — например, поведение груза на пружине. Его фазовыми кривыми являются эллипсы с центром в нуле.
- Пусть — угол, задающий положение точки на единичной окружности. Отображение удвоения , задаёт динамическую систему с дискретным временем, фазовым пространством которой является окружность.
- Быстро-медленные системы описывают процессы, одновременно развивающиеся в нескольких масштабах времени.
- Динамические системы, чьи уравнения могут быть получены посредством принципа наименьшего действия для удобно выбранной функции Лагранжа, известны как "лагранжевы динамические системы".
Вопросы теории динамических систем
Имея какое-то задание динамической системы, далеко не всегда можно найти и описать ее траектории в явном виде. Поэтому обычно рассматриваются более простые (но не менее содержательные) вопросы об общем поведении системы. Например:
- Есть ли у системы замкнутые фазовые кривые, то есть может ли она вернуться в начальное состояние в ходе эволюции?
- Как устроены инвариантные многообразия системы (частным случаем которых являются замкнутые траектории)?
- Как устроен аттрактор системы, то есть множество в фазовом пространстве, к которому стремится «большинство» траекторий?
- Как ведут себя траектории, выпущенные из близких точек — остаются ли они близкими или уходят со временем на значительное расстояние?
- Что можно сказать о поведении «типичной» динамической системы из некоторого класса?
- Что можно сказать о поведении динамических систем, «близких» к данной?
См. также
Ссылки
- Weisstein, Eric W. Dynamical Systems (англ.) на сайте Wolfram MathWorld.
- Нелинейная динамика: подходы, результаты, надежды. М.: УРСС, 2006.
| Статьи, связанные с теорией управления и моделированием | |
|---|---|
| Основные понятия | Динамическая система • Статическая система • Математическая модель • Передаточная функция • Пространство состояний |
| Классификация систем | Линейные стационарные системы (ЛСС) |
| Фундаментальные свойства систем | Устойчивость • Наблюдаемость • Управляемость |
| Другое | Идентификация систем |
| Смежные понятия | Преобразование Лапласа • Z-преобразование • Преобразование Фурье • Дельта-функция |
| Характеристики систем | Импульсная переходная характеристика • АФЧХ • ЛАФЧХ |
| Способы математического описания динамических систем |
Передаточная функция • Пространство состояний |
| Разное | Автоматика и телемеханика • Исследование операций |
| Это заготовка статьи по математике. Вы можете помочь проекту, исправив и дополнив её. |
Tags: Теория динамических систем учебник, теория динамических систем степаньянц, теория динамических систем мгу, теория динамических систем скачать.